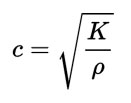Bulk modulus is a term used to describe what happens to a material when uniform isostatic pressure is applied. The polyurethane used here at the Gallagher Corporation has a very high bulk modulus, which means it is virtually incompressible.
Check out our video to see how Bulk Modulus is measured in the Gallagher Corp materials testing lab and why it’s important.
Bulk modulus is a term used to describe what happens to a material when uniform isostatic pressure is applied. The polyurethane used here at the Gallagher Corporation has a very high bulk modulus, which means it is virtually incompressible.
Check out our video to see how Bulk Modulus is measured in the Gallagher Corp materials testing lab and why it’s important.
The bulk modulus K > 0 can be defined by the equation
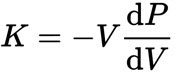
where P is pressure, V is volume, and dP/dV denotes the derivative of pressure with respect to volume.
Equivalently
where ρ is density and dP/dρ denotes the derivative of pressure with respect to density (i.e. pressure rate of change with volume).
The inverse of the bulk modulus gives a substance’s compressibility.
Other moduli describe the material’s response (strain) to other kinds of stress.
The shear modulus describes the response to shear.
Young’s modulus describes the response to linear stress.
Thermodynamic relation
Strictly speaking, the bulk modulus is a thermodynamic quantity, and in order to specify, it is necessary to specify how the temperature varies during compression: constant-temperature (isothermal KT), constant-entropy (isentropic KS), and other variations are possible.
For an ideal gas, the isentropic modulus KS is given by
and the isothermal modulus KT is given by
where
γ is the heat capacity ratio
p is the pressure.
When the gas is not ideal, these equations give only an approximation. In a fluid, K and the density ρ determine the speed of sound c (pressure waves), according to the Newton-Laplace formula
In solids, KS and KT have very similar values. Solids can also sustain transverse waves: for these materials one additional elastic modulus, for example, the shear modulus, is needed to determine wave speeds.
